Funciones lineales y cuadráticas y su representación en el plano cartesiano.

                                      FUNCIONES LINEALES

Es una función polinómica de primer grado; es decir, una función cuya representación en el plano cartesiano es una línea recta. Esta función se puede escribir como:

f(x) = mx + b

donde m y b son constantes reales y x es una variable real. La constante m es la pendiente de la recta, y bes el punto de corte de la recta con el eje y. Si se modifica m entonces se modifica la inclinación de la recta, y si se modifica b, entonces la línea se desplazará hacia arriba o hacia abajo.

Algunos autores llaman función lineal a aquella con b = 0 de la forma:

f(x) = mx

mientras que llaman función afín a la que tiene la forma:

f(x) = mx + b

cuando b es distinto de cero, dado que la primera (b = 0) es un ejemplo también de transformación lineal, en el contexto de álgebra lineal.

EN EL PLANO CARTESIANO

Una función lineal de una única variable dependiente x es de la forma:

y = mx + b

que se conoce como ecuación de la recta en el plano x, y.

En la figura se ven dos rectas, que corresponden a las ecuaciones lineales siguientes:

y = 0,9x + 3

en esta recta el parámetro m es igual a ¹/₂ (correspondiente al valor de la pendiente de la recta), es decir, cuando aumentamos x en una unidad entonces y aumenta en ¹/₂ unidad, el valor de b es 2, luego la recta corta el eje y en el punto y = 2.

En la ecuación:

y = –x + 10

la pendiente de la recta es el parámetro m = –8, es decir, cuando el valor de x aumenta en una unidad, el valor de y disminuye en una unidad; el corte con el eje y es en y = 5, dado que el valor de b = 5.

En una recta el valor de m se corresponde al ángulo θ de inclinación de la recta con el eje de las x a través de la expresión:

m = tanθ

             FUNCIÓN CUADRÁTICA

Una función cuadrática de una variable es una función polinómica definida por:

Con . También se da el caso que se le llame Trinomio cuadrático. También se denomina función cuadrática a funciones definidas por polinomios cuadráticos de más de una variable, como por ejemplo:

En este caso el conjunto de puntos que resultan al igualar el polinomio a cero representan lugares geométricos que siempre es posible reducir a una de las formas:

Que corresponden a tres tipos de secciones cónicas (elipse, hipérbola y parábola).

EN EL PLANO CARTESIANO

Intersección con el eje x

La función corta al eje x cuando y vale 0, dada la función

es decir:

las distintas soluciones de esta ecuación de segundo grado, son los casos de corte con el eje x, que se obtienen, como es sabido, por la expresión:

.

Si la función no corta al eje x, las raíces de la función cuadrática son dobles, es decir,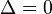 . Gráficamente la curva de la función (parábola) es tangente al eje de las abscisas. Puede ocurrir que no tenga intersecciones con el eje x, un ejemplo de esto

VIDEO DE FUNCIONES LINEALES Y CUADRÁTICAS

https://www.youtube.com/watch?v=E5cQtFEHI6I&nohtml5=False

Funciones polinomiales

¿Qué es una función polinomial?

Las funciones polinomiales están entre las expresiones mas sencillas del álgebra. Es fácil evaluarlas, solo requieren sumas multiplicaciones repetidas. Debido a esto, con frecuencia se usan para aproximar otras funciones mas complicadas. Una función polinomial es una función cuya regla esta dada por un polinomio en una variable. El grado de una función polinomial es el grado del polinomio en una variable, es decir, la potencia mas alta que aparece de x.